Have I gone over to the dark side? Cracked under pressure
Have I gone over to the dark side? Cracked under pressurefrom the REF to resort to fabrication of results to secure that elusive Nature
paper? Or had my brain addled by so many requests for information from ethics
committees that I’ve just decided that its easier to be unethical? Well readers
will be reassured to hear that none of these things is true. What I have to say
concerns the benefits of made-up data for helping understand how to analyse
real data.
In my field of experimental psychology, students get a
thorough grounding in statistics and learn how to apply various methods for
testing whether groups differ from one another, whether variables are
associated and so on. But what they typically don’t get is any instruction in
how to simulate datasets. This may be a historical hangover. When I first
started out in the field, people didn’t have their own computers, and if you
wanted to do an analysis you either laboriously assembled a set of instructions
in Fortran which were punched onto cards and run on a mainframe computer
(overnight if you were lucky), or you did the sums on a pocket calculator. Data
simulation was just unfeasible for most people. Over the years, the
landscape has changed beyond recognition and there are now windows-based
applications that allow one to do complex multivariate statistics at the press
of a button. There is a danger, however, which is that people do analyses
without understanding them. And one of the biggest problems of all is a
tendency to apply statistical analyses post hoc. You can tell people over and
over that this is a Bad Thing (see Gould and Hardin, 2003) but they just don’t get it. A little simulation
exercise can be worth a thousand words.
So here’s an illustration. Suppose we’ve got two groups each
of 10 people, let’s say left-handers and right-handers. And we’ve given them a
battery of 20 cognitive tests. When we scrutinise the results, we find that
they don’t differ on most of the measures, but there’s a test of mathematical
skill on which the left-handers outperform the right-handers. We do a t-test
and are delighted to find that on this measure, the difference between groups is
significant at the .05 level, so we write up a paper entitled "Left-handed advantage for mathematical skills" and submit it to a
learned journal, not mentioning the other 19 tests. After all, they weren’t
very interesting. Sounds OK? Well, it isn’t. We have fallen into the trap of using statistical methods that are valid
for testing a hypothesis that is specified a priori in a situation where the
hypothesis only emerged after scrutinising the data.
Let’s generate some data. Most people have access to
Microsoft Excel, which is perfect for simple simulations. In row 1 we put our
column labels, which are group, var1, var2, …. var 20.
In column A, we then have ten zeroes followed by ten ones, indicating group identity.
We then use random numbers to complete the table. The simplest way to do this
is to just type in each cell:
=RAND()
This generates a random number between 0 and 1.
A more sophisticated option is to generate a random z-score.
This creates random numbers that meet the assumption of many statistical tests
that data are normally distributed. You do this by typing:
=NORMSINV(RAND())
At the foot of each column you can compute the mean and
standard deviation for each group, and Excel automatically computes a p-value
based on the t-test for comparing the groups with a command such as:
=TTEST(B2:B11,B12:B22,2,2)
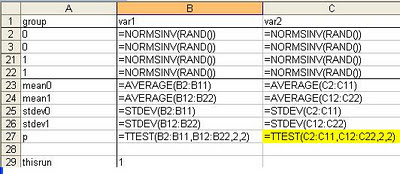
So the formulae in the first three columns look like this (rows 4-20 are hidden):
Copy this formula across all columns. I added conditional formatting
to row 27 so that ‘significant’ p-values are highlighted in yellow (and it
just so happens with this example that the generated data gave a p-value
less than .05 for column C).
Every time you type anything at all on the sheet, all the
random numbers are updated: I’ve just added a row called ‘thisrun’ and typing any number in cell B29 will re-run the simulation. This provides a simple way of generating a
series of simulations and seeing when p-values fall below .05. On some runs,
all the t-tests are nonsignificant, but you’ll quickly see that on many runs
one or more p-values are below .05. In fact, on average, across numerous runs,
the average number of significant values is going to be one because we have twenty columns, and 1/20 = .05. That’s what p <
.05 means! If this doesn’t convince you of the importance of specifying your
hypothesis in advance, rather than selecting data for analysis post hoc,
nothing will.
This is a very simple example, but you can extend the
approach to much more complicated analytic mdthods. It gets challenging in
Excel if you want to generate correlated variables, though if you type a
correlation coefficient in cell A1, and have a random number in column B, and
copy this formula down from cell C2, then columns B and C will be correlated by
the value in cell A1:
=B2*A$1+NORMSINV(RAND())*SQRT(1-A$1^2)
NB, you won’t get the exact correlation on each run: the
precision will increase with the number of rows you simulate.
Other applications, such as Matlab or R, allow you to
generate correlated data more easily. There are examples of simulating multivariate normal datasets in R in my blog on twin methods.
Simulation can be used not just for exploring a whole host
of issues around statistical methods. For instance, you can simulate data to
see how sample size affects results, or how results change if you fail to meet
assumptions of a method. But overall, my message is that data simulation is a
simple and informative approach to gaining understanding of statistical
analysis. It should be used much more widely in training students.
Reference
Good, P. I., & Hardin, J. W. (2003). Common errors in statistics (and how to avoid them). Hoboken, NJ: Wiley.